Bernoulli’s Theorem:
, pressure, and elevation along a streamline. The theorem is based on the conservation of energy for an ideal fluid flowing along a streamline with no external work or heat transfer. The general form of Bernoulli’s theorem is given by:
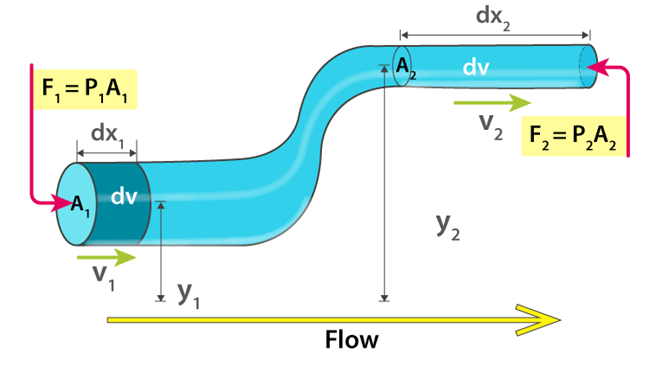
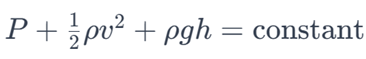
where:
– P is the pressure of the fluid.
– ρ is the density of the fluid.
– v is the velocity of the fluid.
– g is the acceleration due to gravity.
– ℎ is the height above a reference point.
Components of Bernoulli’s Theorem:
1. Pressure Term (P ):
– Represents the static pressure of the fluid.
– Decreases when fluid velocity increases along a streamline.
2. Kinetic Energy Term (1/2 ρ v2):
– Represents the kinetic energy of the fluid.
– Increases when fluid velocity increases along a streamline.
3. Potential Energy Term (ρgh):
– Represents the potential energy due to the elevation of the fluid above a reference point.
– Increases when the fluid is lifted against gravity.
4. Constant:
– The sum of the pressure, kinetic energy, and potential energy along a streamline remains constant in the absence of external forces.
Assumptions of Bernoulli’s Theorem:
1. Steady Flow:
– The fluid flow is steady, meaning it does not change with time.
2. Incompressible Fluid:
– The fluid is assumed to be incompressible, meaning its density remains constant.
3. Non-Viscous Fluid:
– The fluid is considered non-viscous, implying that there is no internal friction or viscosity.
4. No External Work or Heat Transfer:
– The theorem assumes no external work is done on the fluid, and there is no heat transfer.
Applications of Bernoulli’s Theorem:
1. Aeronautics:
– Bernoulli’s theorem explains lift in aerodynamics. Faster-moving air over an airfoil results in lower pressure, causing lift.
2. Venturi Effect:
– The Venturi effect, based on Bernoulli’s theorem, explains the decrease in pressure in a constriction of a fluid flow, such as in a Venturi tube or carburetor.
3. Water Flow in Pipes:
– Bernoulli’s theorem is used to analyze water flow in pipes and to design systems such as water distribution networks.
4. Blood Flow in Arteries:
– The principle is applied to understand blood flow in arteries. Faster blood flow corresponds to lower pressure, helping explain blood circulation.
5. Hydraulic Jumps:
In open channel flow, sudden changes in flow conditions result in hydraulic jumps, and analysts apply Bernoulli’s theorem to analyze such phenomena.
6. Pitot Tubes:
– Pitot tubes, used to measure fluid velocity, utilize Bernoulli’s theorem. The static and dynamic pressures measured help determine fluid velocity.
7. Sprinkler Systems:
Bernoulli’s theorem elucidates the design and operation of sprinkler systems, where nozzles force water to form a spray.
8. Wind Tunnel Design:
In wind tunnel design, engineers use Bernoulli’s theorem to create controlled airflow conditions for aerodynamic testing.
9. Rocket Launch:
Engineers apply the principle to understand the fluid dynamics of rocket launch, where high-speed exhaust gases lead to lower pressure.
10. Siphons:
Bernoulli’s theorem explains how siphons operate, transporting fluid over a crest without the need for any external pump.
Understanding Bernoulli’s theorem is crucial for engineers and scientists working in fluid dynamics, aeronautics, hydraulics, and various other fields. Its applications extend across a wide range of industries, providing insights into the behavior of fluids in different systems.

