Filtration is the process wherein a filter medium separates a heterogeneous mixture of fluid and solid particles. The filter medium allows the passage of fluid but retains the solid particles. The process retains oversized solids in the fluid, but it does not complete the separation, as the filtrate may contaminate with solid particles smaller in size than the pore size of the filter media. This process involves the slurry, which is the suspension of the solid or liquid to be filtered.
The porous medium used to retain the solids is a filter medium.
The filter cake refers to the accumulated solids on the filter media, while the clear liquid passing through the filter is the filtrate.
Filtration is a process used to separate particles and fluid in a suspension where the fluid can be a liquid, a gas, or a supercritical fluid.
Depending on the application, one or both components may be isolated.
Objectives
Its aims to clarify liquor purification.
It aims to separate the solids recovered.
Its aims to separate both the liquids and solids recovered.
It aims to facilitate or improve other plant operations
Applications
- It improves the appearance of various pharmaceutical preparations like solutions, mouthwashes, etc.
- It removes potential irritants; for example, it eliminates irritants from eye drops or solutions used on mucous membranes.
- It removes the turbid products obtained after various unit operations. For example, filtration separates the turbid product from a small quantity of fine suspended colloidal matter obtained by extracting vegetable drugs with a solvent.
- Using a filter that retains the bacteria, this method is employed to detect microorganisms present in liquids. Additionally, this method allows for the evaluation of the efficiency of preservatives.
Theories
The liquid flowing through a filter follows the basic rules governing the flow of any liquid through a medium that offers resistance.
The rate of flow 1s expressed as: Rate = Driving force / Resistance
The following equations can explain the theory of filtration:
1) Poiseuille’s equation,
2) Darcy’s equation, and
3) Kozeny-Carman equation
Poiseuille’s Equation
According to Poiseuille, filtration is similar to the streamlined flow of a liquid
Poiseuille’s equation, named after the French physicist Jean Louis Marie Poiseuille, describes the steady-state laminar flow of an incompressible Newtonian fluid through a cylindrical pipe or vessel. This equation is particularly important in fluid dynamics and is widely used in the study of fluid flow, especially in biological systems, engineering, and medical applications.
Poiseuille’s Equation
The equation is given by:
Q = π Δ P r4 /8 ηl
Where:
– Q is the volumetric flow rate of the fluid.
– Δ P is the pressure drop along the length of the pipe.
r is the radius of the pipe.
η is the dynamic viscosity of the fluid.
– l is the length of the pipe.
Suppose a bulky mass of particles forms a cake and the liquid flows in between the spaces (corresponding to a multiplicity of capillary tubes). In that case, the flow of liquids is expressed by Poiseuille’s equation.
Darcy’s Equation
Poiseuille’s equation considers that non-uniform and highly irregular capillaries are present in the filter. So, if the capillary length is assumed to be the bed (filter medium) thickness, a correction factor for radius is applied to approximate and simplify the rate equation.
Therefore, Darcy incorporated the factor influencing the filtration rate into an equation, which is expressed as:
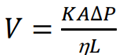
Where
V= Volume of liquid flowing in unit time (m3s)
K=Permeability coefficient of the cake (m2)
A = Surface area of the porous bed (m2)
Δ P = Pressure difference across the filter (Pa)
h= Viscosity of the filtrate (Pa.S)
L=Thickness of the filter cake (capillary length) (m)
Kozeny-Carman Equation
Poiseuille’s equation applies to a porous bed based on a capillary-type structure and other parameters. Thus, the Kozeny-Carman equation is expressed as:
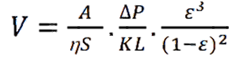
Where,
A = Area of filter medium
S = Specific surface area of the particles comprising the cake (m2/m3)
DP = Pressure drop across the filter medium and the filter cake
K = Kozeny constant
e = Porosity of the cake (bed) Since the flow rate and e3 /(1-e)3 are directly proportional, a 10% change in porosity can change V up to 3-folds
Factors Affecting Filtration
Pressure
Viscosity
Surface area of Filter Media
Temperature
Particle Size
Thickness of Cake
Characteristics of slurry
FILTRATION EQUIPMENT
In the bulk drug industry, solid is the desired product.
Its Size, physical properties, and purity are important
A filter is a device (usually a membrane or layer) designed to physically block certain objects or substances while letting others pass through. Filters are often used to remove solid substances suspended in fluids.

