The half-life of a radioactive substance is the time required for half of the atoms in a given sample to undergo radioactive decay. It is a crucial concept in nuclear physics, medicine, archaeology, and environmental science, as it helps determine the rate of decay of radioactive elements and their persistence in different environments.
Definition of Half-life
The half-life t1/2 of a radioactive substance is defined as the time it takes for half of the radioactive nuclei in a sample to decay into a more stable form. The decay process follows an exponential decay law, meaning that the number of remaining radioactive atoms decreases over time but never reaches zero.
Mathematically, the half-life can be expressed as:

Where:
t1/2 = half-life of the substance
λ = decay constant (probability of decay per unit time)
2. Exponential Decay Law
The number of radioactive nuclei N at time t is given by the equation:
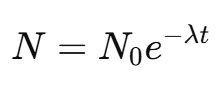
Where:
N0 = initial number of radioactive atoms
N = number of radioactive atoms remaining at time \( t \)
λ = decay constant
t = time elapsed
I = Euler’s number (≈ 2.718)
Using the half-life formula, we can derive the decay equation for any radioactive element.
3. Graphical Representation of Half-life
A radioactive decay curve shows the number of remaining radioactive nuclei as a function of time. The key characteristics of this curve include:
It starts with N0, the original number of radioactive atoms.
At t = t1/2, half of the atoms have decayed, leaving N0/2.
At 2t1/2, only N0/4 atoms remain.
This pattern continues, reducing the number of radioactive atoms by half with each half-life.
Example Calculation
Suppose a radioactive isotope has a half-life of 10 hours, and we start with 100 g of the substance.
After:
10 hours → 50 g remains.
20 hours → 25 g remains.
30 hours → 12.5 g remains.
40 hours → 6.25 g remains.
This illustrates the exponential nature of radioactive decay.
4. Factors Affecting Half-life
Unlike chemical reactions, the half-life of a radioactive substance is not affected by:
Temperature
Pressure
Catalysts
Physical state (solid, liquid, or gas)
This is because radioactive decay is governed by nuclear forces, which are independent of external conditions.
5. Applications of Half-life
A. Radiocarbon Dating (Carbon-14 Dating): Used in archaeology and geology to determine the age of ancient artifacts, fossils, and remains. Carbon-14 (14C^{14}C14C) has a half-life of 5,730 years and is used to date organic materials.
B. Nuclear Medicine: Used in medical imaging and treatment of diseases.
Example: Technetium-99m (99mTc^{99m}Tc99mTc) has a half-life of 6 hours, making it ideal for medical scans.
C. Nuclear Power Plants: Half-life helps determine the long-term management of nuclear waste.
Example: Uranium-235 (235U^{235}U235U) has a half-life of 703.8 million years.
D. Environmental Science: Used to monitor radioactive contamination.
Example: Cesium-137 (137Cs^{137}Cs137Cs) from nuclear fallout has a half-life of 30 years.
E. Space Exploration: Radioisotope thermoelectric generators (RTGs) use long-lived isotopes like Plutonium-238 (238Pu^{238}Pu238Pu, half-life = 87.7 years) to power spacecraft.
6. List of Common Radioactive Isotopes and Their Half-lives
| Isotope | Half-life | Application |
|---|---|---|
| Carbon-14 (14C^{14}C14C) | 5,730 years | Radiocarbon dating |
| Uranium-238 (238U^{238}U238U) | 4.5 billion years | Geological dating |
| Iodine-131 (131I^{131}I131I) | 8 days | Thyroid treatment |
| Radon-222 (222Rn^{222}Rn222Rn) | 3.8 days | Radiation hazard monitoring |
| Strontium-90 (90Sr^{90}Sr90Sr) | 28.8 years | Radiation therapy |
Conclusion
The half-life of a radioactive substance is a fundamental concept that explains the exponential nature of radioactive decay. It has significant implications in various scientific fields, from medicine and archaeology to nuclear energy and environmental protection. Understanding half-life allows us to harness radioactive materials safely and effectively for technological advancements.

